本网讯（通讯员 杨新宇）7月31日至8月4日，应公司程勇教授邀请， 比利时根特大学数学系Andreas Weiermann教授来公司振华楼B214作了连续五场“具体不完全性”的系列讲座。讲座形式采用线上线下混合形式，通过Bilibili和Zoom平台向海内外观众直播，每场讲座平均超过350名观众参与，本系列讲座由程勇教授主持。著名逻辑学家Harvey Friedman也在Zoom平台参与了讲座。

Andreas. Weiermann教授是国际知名逻辑学家，是证明论和具体不完全性领域的领军人物，本系列讲座以证明论及序数分析的进路介绍具体不完全性，从证明论的基本结果出发，以可证递归函数的分层定理为工具，证明了Paris-Harrington和Friedman等构造的组合语句相对于Peano算术的不可证性，并讨论了从可证性到不可证性的“相变”（phase transition）问题。

在第一场讲座中，Weiermann教授回顾了数理逻辑的发展史，将具体不完全性研究置于数学基础研究的关键位置，突显了该领域的重要意义。随后Weiermann教授回顾了谓词逻辑的Cut-elimination定理这一经典结果，为之后的讲座作了技术准备。

在第二场讲座中，Weiermann教授讲授了Peano算术的证明论。Weiermann教授将不超过ϵ₀的良序以有穷数列的哥德尔编码表示，从而证明了对于任意小于ϵ₀的序数的归纳原则在Peano算术中都是可证的。基于这一事实，Weiermann教授证明了对于递归函数的Hardy分层，下标小于ϵ₀的Hardy函数在Peano算术中都是可证递归的，即Peano算术可以证明其是全函数。另一方面，下标为ϵ₀的Hardy函数却不是可证递归的。为了建立这一结果，Weiermann教授通过对添加Buchholz控制算子的无穷推演形式的Peano算术的序数分析证明了归约引理(Reduction Lemma), 进而得到了Hardy函数相对于Buchholz控制算子的有界性。

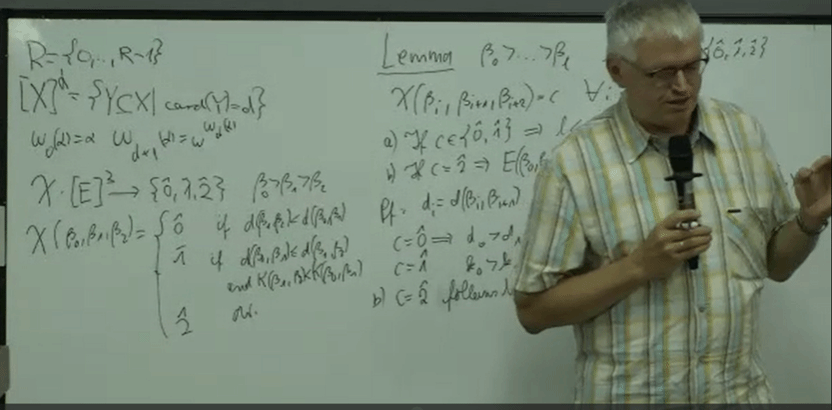
在第三场讲座中，Weiermann教授给出了Paris-Harrington语句不可证性的完整证明。与文献中已有的经典证明不同，Weiermann教授直接在序数标记(ordinal notation)上应用Ramsey理论，以序数的秩为工具，构造了一个巧妙的染色函数，得到了Hardy函数相对于Paris-Harrington函数的有界性。 由下标为ϵ₀的Hardy函数非可证递归这一结论得到了Paris-Harrington语句不可证性。

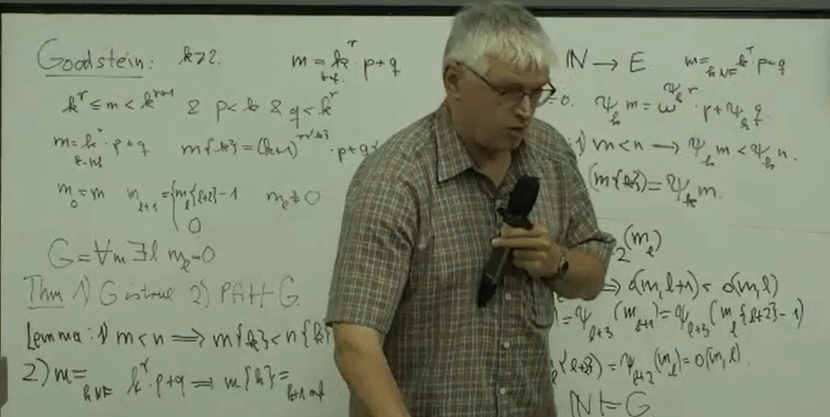
在第四场讲座中，Weiermann教授基于下标等于ϵ₀的Hardy函数非Peano算术可证递归这一结论证明了Friedman式的若干组合语句（Hydra博弈的必胜性（H）、ϵ₀的缓慢良序性（SWO）、有穷树的Kruskal定理（FKT））相对于Peano算术的不可证性。并且Weiermann教授还基于Hydra博弈的必胜性的不可证性证明了Goodstein序列终止性的不可证性。

在第五场讲座中，Weiermann教授讨论了上一讲中得到的不可证语句的“相变”问题：即若某个特定的组合数学定理附带一个递增函数为参数，这个函数增长速度快到何种程度可以使其在Peano算术中不可证。Weiermann教授以解析组合学(analytical combinatoric)和复分析为工具，讨论了组合语句H、SWO和FKT的相变问题。

本系列讲座深入浅出，既易于一般的数理逻辑学习者入门具体不完全性这一领域，又深刻诠释了数理逻辑同数学其他领域的密切联系，反映了不可证现象背后的数学本质。在一些经典结果的证明上，Weiermann教授往往另辟蹊径，将序数这一工具使用得出神入化，令人耳目一新、拍案称奇。

（编辑：邓莉萍   审稿：严璨）